¿Cuál es la importancia de comprender cómo se calcula la pendiente entre dos puntos?
Calcular la pendiente entre dos puntos es un concepto fundamental en matemáticas y ciencias aplicadas. Ya sea que estés estudiando geometría en la escuela o trabajando en un proyecto de ingeniería civil, conocer cómo determinar la pendiente te ayudará a comprender mejor las relaciones espaciales y la inclinación entre distintos puntos en un plano cartesiano.
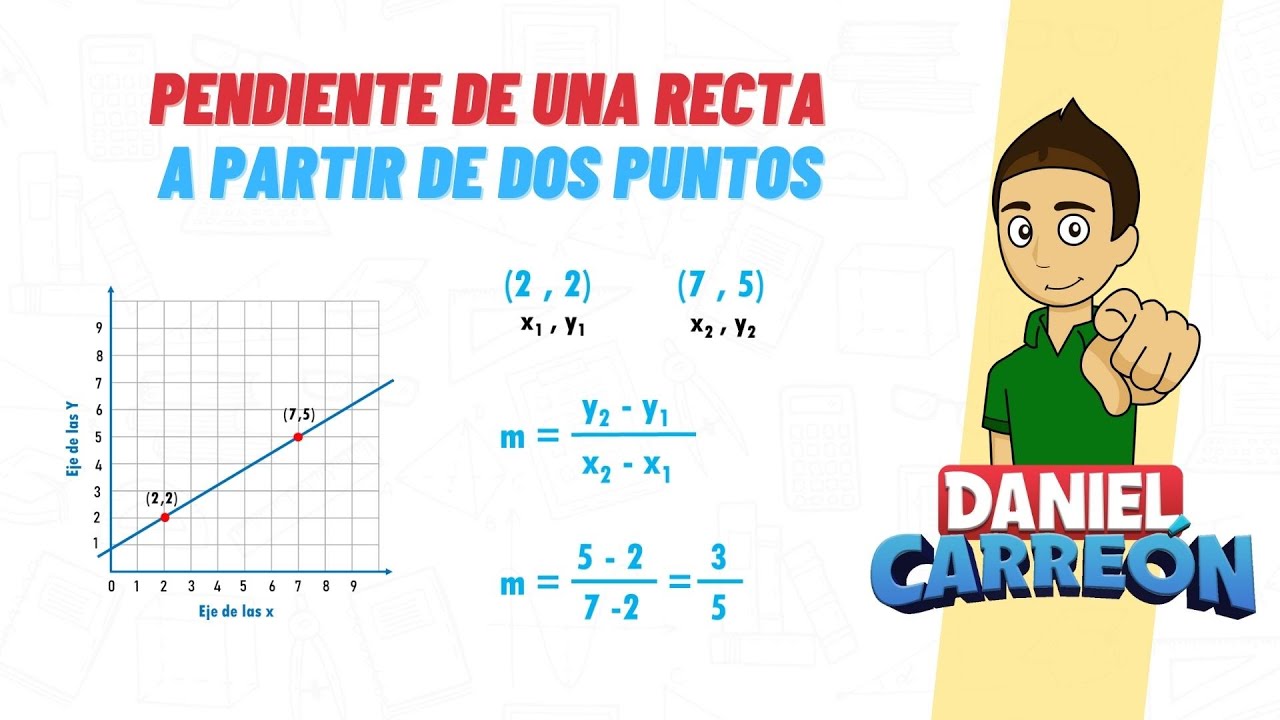
Identificando los puntos en el plano cartesiano
Antes de poder calcular la pendiente entre dos puntos, es crucial identificar las coordenadas de los puntos en el plano cartesiano. Cada punto estará representado por un par ordenado (x,y), donde ‘x’ es la coordenada en el eje horizontal (eje de las x) y ‘y’ es la coordenada en el eje vertical (eje de las y).
Fórmula para calcular la pendiente
Una vez que tengas las coordenadas de los dos puntos que deseas analizar, puedes aplicar la fórmula para calcular la pendiente. La fórmula básica para hallar la pendiente (m) entre dos puntos (x1,y1) y (x2,y2) es:
m = (y2 – y1) / (x2 – x1)
Aplicación de la fórmula
Imagina que tienes los puntos (2,3) y (5,9) y deseas encontrar la pendiente entre ellos. Sustituyendo los valores en la fórmula, obtendrás:
m = (9 – 3) / (5 – 2)
m = 6 / 3 = 2
Por lo tanto, la pendiente entre los puntos (2,3) y (5,9) es 2. Esto significa que la recta que une estos dos puntos tiene una inclinación de 2 unidades en el eje vertical por cada unidad en el eje horizontal.
Interpretación geométrica de la pendiente
La pendiente no solo es un valor numérico, sino que también tiene una interpretación geométrica. Una pendiente positiva indica una inclinación hacia arriba de izquierda a derecha, mientras que una pendiente negativa representa una inclinación descendente en la misma dirección. Una pendiente de cero significa una línea horizontal.
Utilizando la pendiente en el mundo real
En campos como la topografía, la ingeniería y la física, el concepto de pendiente es fundamental para diseñar estructuras, calcular gradientes y comprender el movimiento de objetos en un plano. Por lo tanto, dominar cómo se calcula la pendiente entre dos puntos te brindará una sólida base para abordar problemas más complejos en estas áreas.
1. ¿Por qué es importante considerar la pendiente al diseñar una carretera?
2. ¿Cómo se relaciona la pendiente con la velocidad de un objeto en movimiento?
3. ¿Cuál es la diferencia entre la pendiente y la tangente en términos geométricos?
¡Explora más sobre este fascinante tema y profundiza en tus conocimientos matemáticos y científicos!