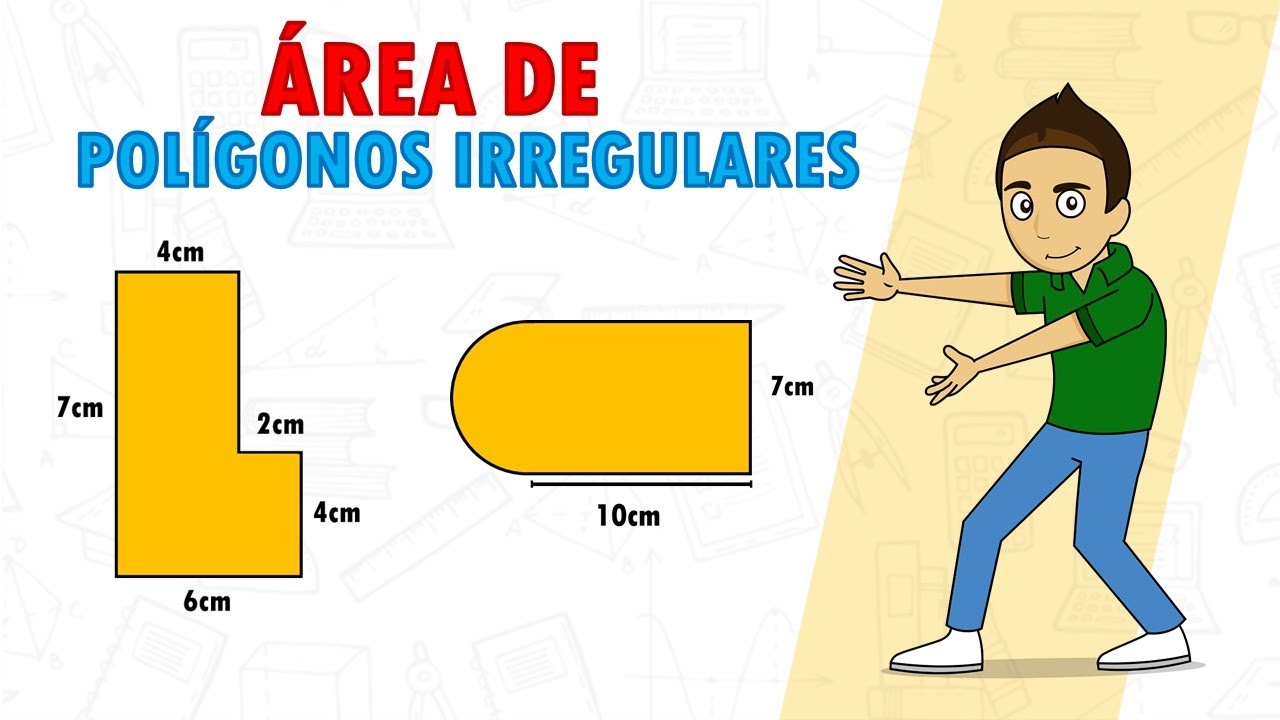
En el excitante mundo de la geometría, muchas veces nos enfrentamos a desafíos al tratar de calcular el perímetro y área de figuras irregulares. Afortunadamente, con los conocimientos y herramientas adecuadas, podemos resolver estas incógnitas de forma sencilla y precisa. En esta guía paso a paso, te mostraremos cómo abordar estos cálculos con confianza y precisión, brindándote el poder de dominar figuras que desafían lo convencional.
Descubre los Secretos para Calcular el Perímetro de Figuras Irregulares
El perímetro de una figura irregular puede parecer una incógnita compleja, pero en realidad, se reduce a la suma de las longitudes de todos sus lados. Para calcular con éxito el perímetro, necesitarás identificar cada lado de la figura y sumar sus longitudes. Este proceso puede variar según la forma de la figura, por lo que es fundamental desglosarla en segmentos más simples para facilitar el cálculo.
Identificar los Lados de la Figura
Para comenzar, observa detenidamente la figura irregular y descomponla en segmentos rectos o curvos, identificando claramente cada lado. En caso de que la figura tenga lados curvos, puedes subdividirlos en tramos rectos aproximados para simplificar el cálculo. Una vez que hayas realizado esta división, mide la longitud de cada lado utilizando una regla o cinta métrica.
Sumar las Longitudes de los Lados
Con las longitudes de todos los lados en mano, simplemente suma estos valores para obtener el perímetro total de la figura irregular. Recuerda tener en cuenta las unidades de medida utilizadas para expresar el perímetro, ya sea en centímetros, metros, pulgadas, o la unidad que corresponda según el sistema de medición empleado. ¡Ya estás un paso más cerca de descifrar los secretos de esta enigmática figura!
Domina el Arte de Calcular el Área de Figuras Irregulares
Si bien el perímetro nos brinda información sobre la longitud de los lados de una figura, el área nos revela la extensión de su superficie, proporcionando un conocimiento más profundo sobre su composición y tamaño. Calcular el área de una figura irregular puede parecer desafiante, pero con algunas técnicas simples y un enfoque metódico, podrás desentrañar este misterio geométrico con facilidad.
Determinar la Composición de la Figura
Antes de empezar a calcular el área, analiza la figura irregular y visualiza cómo puede dividirse en secciones más simples, como triángulos, rectángulos o trapecios. Identificar estas secciones te permitirá aplicar fórmulas específicas para encontrar el área de cada una y luego sumarlas para obtener el área total de la figura. Este enfoque desglosado simplificará enormemente el proceso de cálculo.
Aplicar Fórmulas de Área
Una vez que hayas dividido la figura en secciones manejables, aplica las fórmulas de área correspondientes a cada forma geométrica involucrada. Por ejemplo, para encontrar el área de un triángulo, puedes utilizar la fórmula A = 1/2 * base * altura, mientras que para un rectángulo o cuadrado, la fórmula es simplemente A = base * altura. Calcula el área de cada sección y luego suma estos valores para obtener el área total de la figura irregular.
¿Existen fórmulas generales para calcular el perímetro y área de todas las figuras irregulares?
No hay una fórmula única que aplique a todas las figuras irregulares, ya que cada una puede tener una composición distinta. Es fundamental identificar las secciones más simples de la figura para aplicar las fórmulas adecuadas y obtener resultados precisos.
¿Es importante tener en cuenta las unidades de medida al calcular el perímetro y área?
Sí, es crucial mantener la coherencia en las unidades de medida utilizadas para evitar confusiones al expresar el perímetro y área de la figura. Asegúrate de utilizar la misma unidad de medida para todos los lados y dimensiones involucradas en los cálculos.
¿Cómo puedo comprobar que mis cálculos de perímetro y área son correctos?
Una forma de verificar la precisión de tus cálculos es dividir la figura en secciones conocidas, calcular el perímetro y área de cada sección por separado y luego comparar estos valores con los obtenidos inicialmente para la figura completa. Si los resultados coinciden, es probable que tus cálculos sean correctos.