Cuando nos enfrentamos a figuras geométricas, a menudo nos encontramos con la necesidad de calcular las diagonales para resolver problemas específicos. Con esta completa guía paso a paso, aprenderás de forma sencilla y clara cómo sacar las diagonales de cualquier figura. ¡Prepárate para sumergirte en el fascinante mundo de la geometría y descubrir todo lo que necesitas saber!
¿Por qué son importantes las diagonales en una figura geométrica?
Antes de adentrarnos en el proceso de cálculo, es fundamental comprender la relevancia de las diagonales en una figura geométrica. Las diagonales no solo nos brindan información sobre la estructura y propiedades de la figura, sino que también son clave para resolver diversos problemas matemáticos. Al conocer cómo sacar las diagonales, ampliamos nuestro entendimiento de las formas y sus características, lo que resulta fundamental en ámbitos como la arquitectura, la ingeniería y la física.
Iniciando el proceso: Paso a paso para calcular las diagonales
Paso 1: Identifica el tipo de figura
El primer paso para determinar las diagonales de una figura es identificar su tipo. Ya sea un triángulo, un cuadrilátero, un pentágono u otra forma poligonal, cada una requiere un enfoque específico para calcular sus diagonales. Examina la figura con atención y define su naturaleza geométrica.
Paso 2: Encuentra el número de vértices
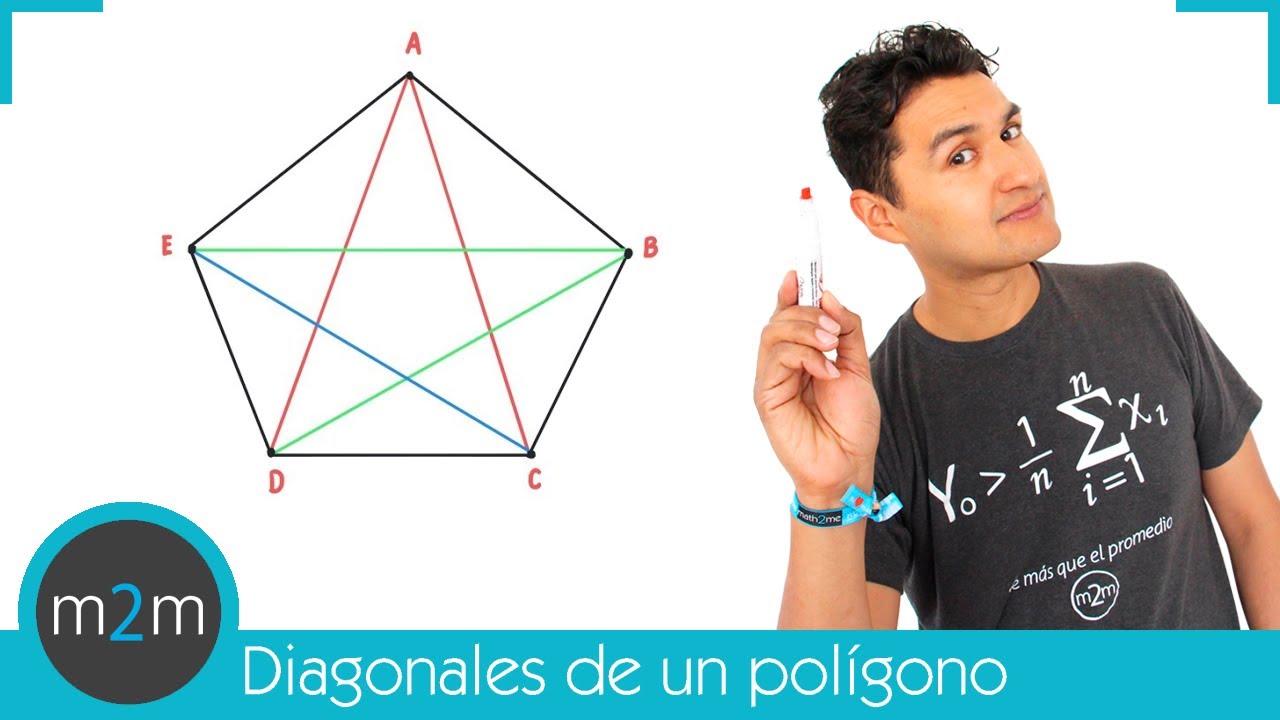
Una vez que has determinado el tipo de figura, es importante contar el número de vértices que posee. Este dato es fundamental para calcular de manera precisa las diagonales, ya que cada vértice puede estar conectado a otros mediante dichas líneas.
Paso 3: Aplica la fórmula correspondiente
Según la figura con la que estás trabajando, existen fórmulas específicas para calcular las diagonales. Por ejemplo, en un cuadrilátero, la fórmula para obtener el número de diagonales es (n * (n – 3)) / 2, donde «n» representa el número de vértices. Asegúrate de utilizar la fórmula correcta para la figura en cuestión.
Explorando casos prácticos y ejemplos
Caso 1: Triángulo equilátero
En un triángulo equilátero, todas las diagonales son iguales y pueden ser calculadas mediante una relación trigonométrica simple. Utilizando el teorema de Pitágoras, podrás determinar la longitud de cada diagonal con facilidad.
Caso 2: Cuadrado
En un cuadrado, las diagonales son perpendiculares entre sí y se cruzan en ángulos de 90 grados. Conocer la longitud de un lado te permitirá calcular la longitud de las diagonales utilizando el teorema de Pitágoras o el teorema de la bisectriz.
Consideraciones finales y recomendaciones adicionales
Al finalizar el proceso de cálculo de las diagonales, es importante revisar tus resultados y asegurarte de haber aplicado correctamente las fórmulas correspondientes. Siempre verifica tus cálculos y, en caso de duda, no dudes en consultar recursos adicionales o profesionales en el campo de la geometría.
¿Cómo afecta el número de vértices al cálculo de diagonales?
El número de vértices en una figura determina la cantidad de posibles combinaciones de líneas diagonales que pueden trazarse. Cuantos más vértices tenga la figura, mayor será la complejidad del cálculo de diagonales.
¿Existen casos en los que una figura no tenga diagonales?
Existen figuras geométricas específicas, como el círculo, que no poseen diagonales debido a su estructura circular y simétrica. En estos casos, el concepto de diagonales no aplica y es importante reconocer las peculiaridades de cada forma.