En esta guía práctica te enseñaré paso a paso cómo encontrar los ángulos de un triángulo, un concepto fundamental en geometría. Comprender cómo calcular los ángulos de un triángulo es esencial para resolver problemas matemáticos y aplicaciones prácticas en la vida cotidiana. Sigue leyendo para dominar esta habilidad con facilidad y precisión.
Conceptos básicos sobre los ángulos de un triángulo
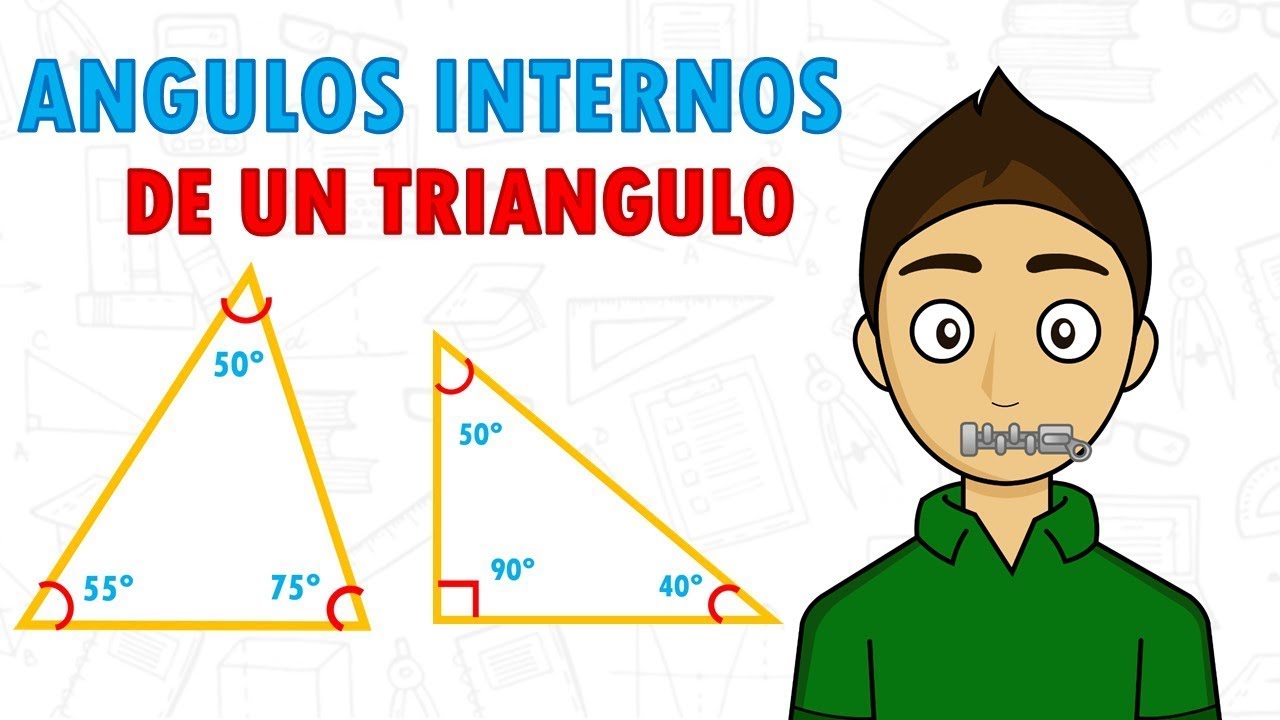
Antes de sumergirnos en los cálculos específicos, es importante entender algunos conceptos básicos sobre los ángulos de un triángulo. Un triángulo consta de tres lados y tres ángulos internos que siempre suman 180 grados. Estos ángulos pueden variar en medida dependiendo del tipo de triángulo que estemos analizando, ya sea equilátero, isósceles o escaleno. Además, cada uno de los ángulos en un triángulo tiene una relación única con los otros, lo que nos permite encontrar su medida de manera precisa mediante diversas fórmulas y reglas matemáticas.
Paso 1: Identificar el tipo de triángulo
El primer paso para encontrar los ángulos de un triángulo es identificar el tipo de triángulo del que estamos hablando. Un triángulo equilátero tiene todos sus lados iguales y, por lo tanto, todos sus ángulos son iguales, midiendo 60 grados cada uno. En un triángulo isósceles, dos de sus lados son iguales, lo que implica que dos de sus ángulos también serán iguales. Por último, un triángulo escaleno tiene todos sus lados y ángulos diferentes, lo que requiere un enfoque más detallado para encontrar sus medidas angulares.
Paso 2: Aplicar la suma de ángulos de un triángulo
Una vez que hayamos identificado el tipo de triángulo, podemos aplicar la regla de la suma de los ángulos internos de un triángulo, que establece que la suma de los tres ángulos internos siempre es igual a 180 grados. Esta regla fundamental nos permite resolver ecuaciones simples para determinar la medida de cada uno de los ángulos en función de los datos que se nos proporcionen sobre el triángulo en cuestión. Al aplicar esta regla, podemos despejar incógnitas y calcular los ángulos de manera eficiente.
Paso 3: Utilizar la ley del seno y del coseno
En casos más complejos, donde no contamos con la información suficiente para aplicar directamente la suma de los ángulos internos, podemos recurrir a la ley del seno y del coseno. Estas leyes trigonométricas nos permiten relacionar los lados y ángulos de un triángulo de manera más amplia, facilitando el cálculo de ángulos en situaciones donde la geometría básica no es suficiente. Al dominar estas leyes, ampliamos nuestras herramientas matemáticas para resolver problemas geométricos de mayor complejidad con precisión y claridad.
Paso 4: Verificar la congruencia de triángulos
Finalmente, es crucial verificar la congruencia de los triángulos al calcular sus ángulos. Dos triángulos son congruentes cuando tienen los mismos lados y ángulos, aunque puedan estar dispuestos en diferentes posiciones. Al aplicar criterios de congruencia como el lado-lado-lado (LLL), lado-ángulo-lado (LAL) o ángulo-lado-ángulo (ALA), podemos asegurarnos de que nuestros cálculos sean precisos y que los ángulos determinados correspondan correctamente al triángulo en cuestión.
¿Qué sucede si la suma de los ángulos de un triángulo no es igual a 180 grados?
Si la suma de los ángulos de un triángulo no alcanza los 180 grados, es posible que se trate de un triángulo curvo o que los ángulos no estén siendo medidos de manera precisa. En estos casos, es importante revisar cuidadosamente los cálculos y la geometría del triángulo para identificar posibles errores.
¿Cómo puedo determinar los ángulos de un triángulo sin conocer la longitud de sus lados?
Si solo se nos proporciona información sobre los ángulos de un triángulo y no sobre la longitud de sus lados, podemos utilizar las propiedades trigonométricas y las relaciones angulares para calcular los ángulos internos. La ley del seno y del coseno son herramientas valiosas en estos casos, permitiéndonos encontrar medidas angulares con base en las proporciones y relaciones geométricas del triángulo.