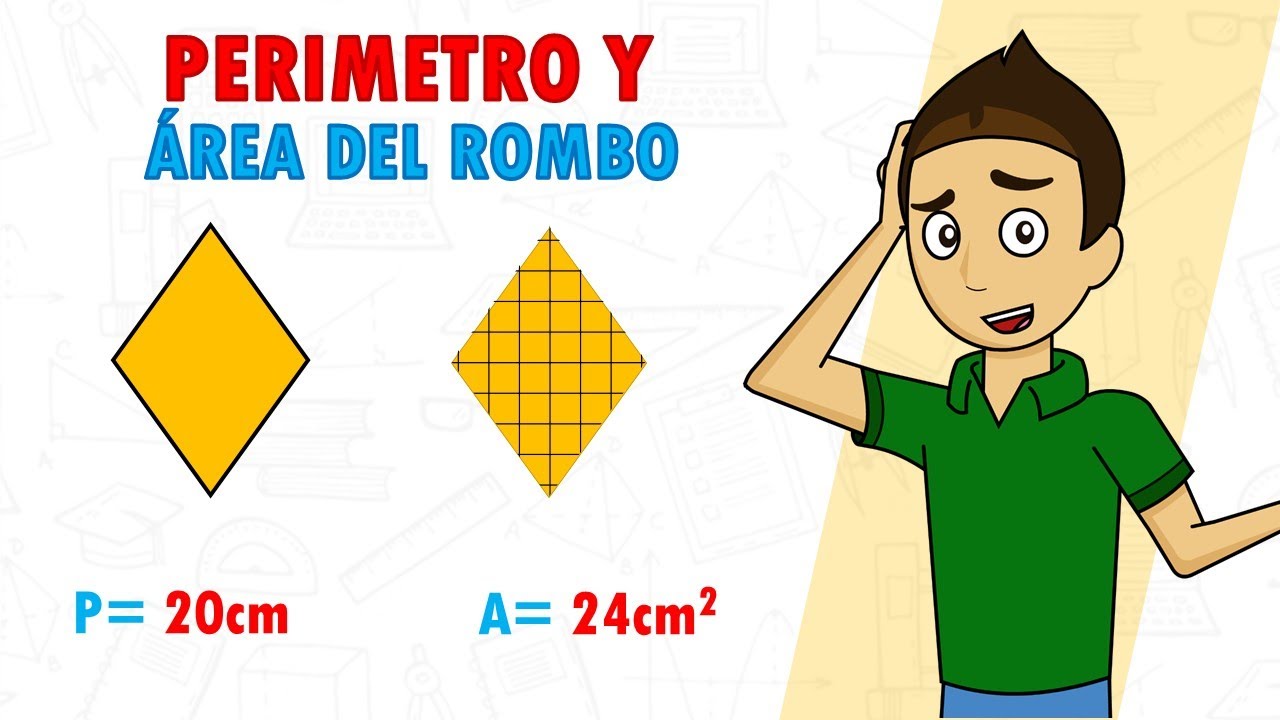
¿Qué es un rombo y por qué es importante saber cómo calcular su área y perímetro?
Un rombo es un cuadrilátero con lados de igual longitud y ángulos opuestos iguales. Es una figura geométrica interesante por su simetría y propiedades únicas. Calcular el área y perímetro de un rombo es fundamental en matemáticas y ciencias, ya que nos permite comprender mejor conceptos como la geometría, la trigonometría y la física. Además, saber cómo encontrar estas medidas nos ayuda en la resolución de problemas prácticos en la vida cotidiana y en campos como la arquitectura, la ingeniería y la carpintería.
Paso 1: Comprender la fórmula del área de un rombo
El área de un rombo se puede calcular multiplicando la longitud de sus diagonales y dividiendo el resultado entre 2. Si denotamos a las diagonales como d1 y d2, la fórmula para el área (A) sería: A = (d1 * d2) / 2. Es importante recordar que las diagonales de un rombo siempre se intersecan en ángulos perpendiculares.
Paso 1.1: Obtener las longitudes de las diagonales
Para calcular el área de un rombo, es crucial conocer la longitud de ambas diagonales. Generalmente, en un problema dado, se proporcionarán las medidas de las diagonales o será necesario medirlas utilizando una regla, cinta métrica o instrumentos de medición. Asegúrate de que las longitudes estén en la misma unidad de medida.
Paso 1.2: Aplicar la fórmula del área
Una vez que tengas las medidas de las diagonales, simplemente sustitúyelas en la fórmula del área del rombo y realiza la operación matemática para obtener el valor del área en unidades cuadradas. Este cálculo te dará la superficie encerrada por el rombo, lo que resulta útil al trabajar con materiales o áreas de superficie en proyectos de construcción o diseño.
Paso 2: Calcular el perímetro de un rombo
El perímetro de un rombo es la suma de las longitudes de sus cuatro lados. Dado que los lados de un rombo son iguales, podemos simplificar la fórmula del perímetro (P) como: P = 4 * lado, donde «lado» representa la longitud de cualquiera de los lados del rombo.
Paso 2.1: Conocer la longitud de un lado del rombo
Al igual que en el caso de las diagonales, es esencial tener la medida de al menos un lado del rombo para calcular su perímetro. Esta medida suele ser proporcionada en un enunciado o se puede obtener mediante la medición directa en el caso de figuras físicas. Asegúrate de que la unidad de medida sea coherente con la de las diagonales si estás trabajando con diferentes sistemas de unidades.
Paso 2.2: Aplicar la fórmula del perímetro
Una vez que conoces la longitud de un lado del rombo, simplemente multiplica ese valor por 4 para obtener el perímetro total de la figura. Este cálculo te dará la medida de la longitud total de los cuatro lados del rombo, lo que es vital para determinar la cantidad de material perimetral necesaria en proyectos de cercados, enmarcado de cuadros u otras aplicaciones prácticas.
¿Cómo se diferencia un rombo de un cuadrado en términos de área y perímetro?
Un rombo tiene todos sus lados iguales pero sus ángulos no necesariamente son de 90 grados, mientras que un cuadrado tiene todos sus lados y ángulos iguales. Esto afecta tanto el cálculo del área como del perímetro de cada figura.
¿Por qué es importante conocer la fórmula del área y perímetro de un rombo en la vida cotidiana?
Saber cómo calcular el área y perímetro de un rombo puede ser útil en situaciones cotidianas como el diseño de patios, la instalación de azulejos en un formato romboidal o la elaboración de artesanías geométricas.
¿Existen métodos alternativos para calcular el área y perímetro de un rombo?
Además de las fórmulas tradicionales, el área de un rombo también se puede encontrar utilizando la fórmula de Herón si se conocen las longitudes de los lados. El perímetro puede calcularse sumando las distancias de sus vértices al centro del rombo y multiplicando por 4.
Este artículo ha proporcionado una guía detallada sobre cómo calcular el área y perímetro de un rombo paso a paso. Con esta información, podrás aplicar tus conocimientos matemáticos en la resolución de problemas prácticos y en la comprensión de conceptos geométricos fundamentales. ¡Sigue explorando el fascinante mundo de la geometría y sus aplicaciones en la vida real!