Calcular la pendiente de una recta es un concepto clave en matemáticas que puede resultar desafiante para algunos estudiantes. Sin embargo, con la orientación adecuada y una comprensión clara de los pasos involucrados, dominar este concepto se vuelve más accesible de lo que parece. En esta guía paso a paso, exploraremos detalladamente cómo obtener la pendiente de una recta y brindaremos ejemplos prácticos para ayudarte a consolidar tu comprensión.
¿Qué es la pendiente de una recta y por qué es importante?
La pendiente de una recta es una medida que indica la inclinación o la tasa de cambio de la recta en un plano cartesiano. Es fundamental en matemáticas y ciencias, ya que proporciona información crucial sobre la dirección y la magnitud del cambio en una función lineal. Imagina la pendiente como la «pronunciación» de una recta: te dice cuán empinada es en relación con los ejes x e y.
¿Cómo se calcula la pendiente de una recta?
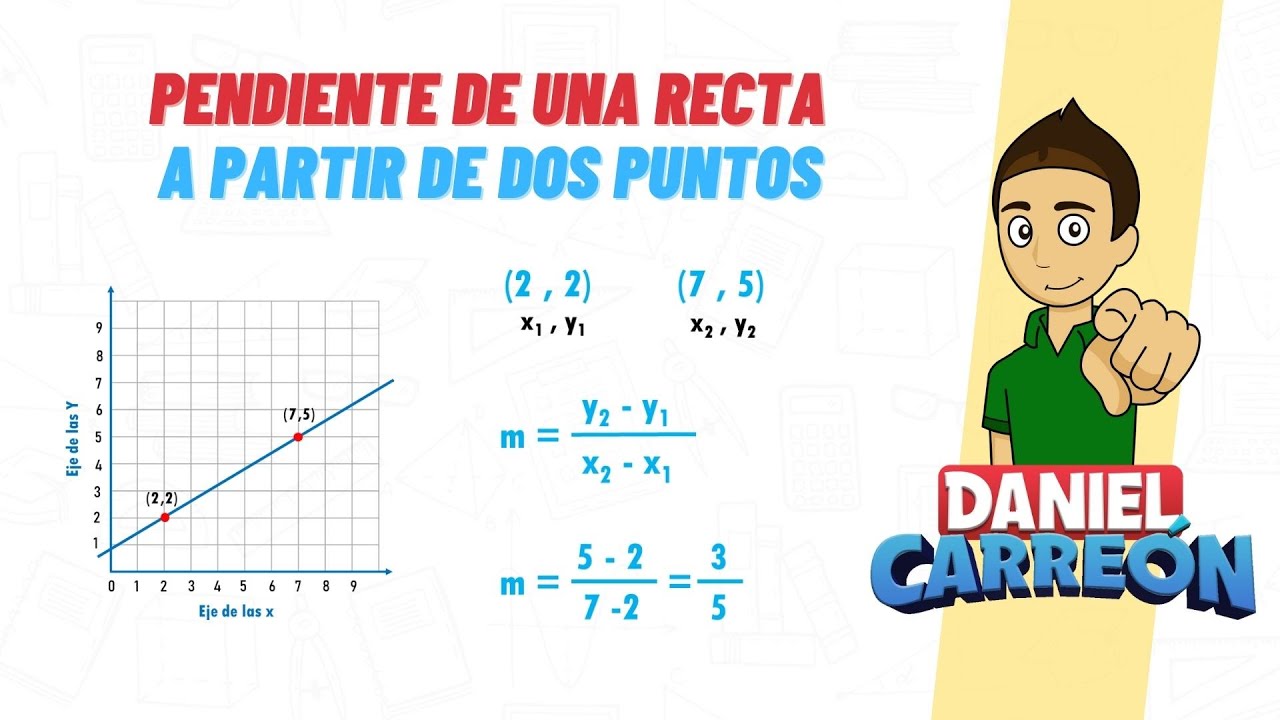
Para calcular la pendiente de una recta, necesitamos dos puntos distintos en la recta. Estos puntos se suelen denotar como P1 (x1, y1) y P2 (x2, y2). La fórmula general para determinar la pendiente (m) es:
m = (y2 – y1) / (x2 – x1)
Esta fórmula se conoce como la «fórmula de la pendiente» y es la base para calcular este importante concepto matemático. Veamos paso a paso cómo aplicar esta fórmula en la práctica para obtener la pendiente de una recta.
Pasos para calcular la pendiente de una recta:
Paso 1: Identificar los puntos dados en la recta
El primer paso es encontrar los dos puntos que se utilizan para calcular la pendiente. Estos puntos deben tener coordenadas claras en el plano cartesiano, por ejemplo, P1 (2, 3) y P2 (5, 9).
Paso 2: Sustituir las coordenadas en la fórmula de la pendiente
Una vez identificados los puntos, sustituimos sus coordenadas en la fórmula de la pendiente. Siguiendo la fórmula m = (y2 – y1) / (x2 – x1), calculamos la diferencia entre las coordenadas y luego dividimos para obtener el valor de la pendiente.
Paso 3: Simplificar el cálculo de la pendiente
Es importante simplificar el resultado para expresar la pendiente de forma clara y concisa. También es crucial verificar que los cálculos se han realizado correctamente para evitar errores en el resultado final.
Paso 4: Interpretar el valor de la pendiente
Una vez obtenida la pendiente, es fundamental interpretar su valor. Una pendiente positiva indica una inclinación hacia arriba de izquierda a derecha, mientras que una pendiente negativa sugiere una inclinación descendente en la misma dirección. Un valor de pendiente de 0 representa una recta horizontal.
Al dominar estos pasos y practicar con diversos ejemplos, podrás desarrollar una sólida comprensión de cómo obtener la pendiente de una recta y aplicar este conocimiento en diferentes contextos matemáticos y científicos.
¿Por qué es importante conocer la pendiente de una recta en matemáticas?
La pendiente de una recta es fundamental en el análisis de funciones lineales, ya que proporciona información crucial sobre la tasa de cambio y la dirección de una recta en el plano cartesiano. Comprender este concepto es esencial para resolver problemas de geometría, álgebra y cálculo.
¿Cómo puedo mejorar mi habilidad para calcular la pendiente de una recta?
La práctica constante es clave para mejorar tus habilidades matemáticas. Realiza ejercicios variados que impliquen el cálculo de la pendiente y busca recursos educativos adicionales, como tutoriales en línea o libros de texto, para reforzar tu comprensión del tema.
¿Existen aplicaciones o herramientas que faciliten el cálculo de la pendiente de una recta?
Sí, actualmente existen numerosas aplicaciones y herramientas en línea que te permiten calcular la pendiente de una recta de forma rápida y precisa. Estas herramientas pueden ser útiles para verificar tus cálculos o resolver problemas matemáticos de manera eficiente.