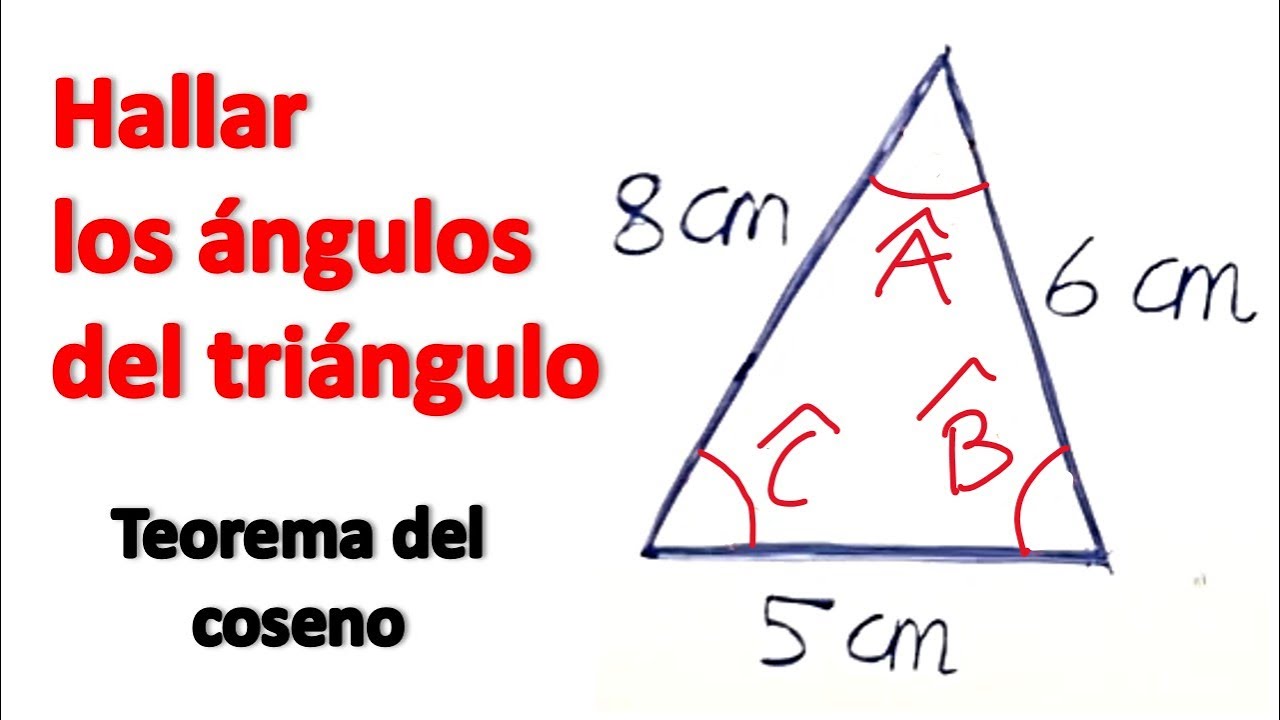
¿Qué son los ángulos de un triángulo?
Un triángulo, figura geométrica formada por tres segmentos de recta que se unen en tres vértices, tiene una serie de propiedades matemáticas que lo definen por completo, una de ellas son sus ángulos. Conocer los ángulos de un triángulo es vital en geometría y resuelve muchos problemas dentro de esta rama de las matemáticas. En este artículo, te guiaremos paso a paso para que aprendas a obtener los ángulos de un triángulo cuando conoces la longitud de sus lados.
Paso 1: Conocer la suma de los ángulos de un triángulo
Antes de adentrarnos en el cálculo de los ángulos individuales de un triángulo, es esencial recordar que la suma de los tres ángulos internos de cualquier triángulo siempre será igual a 180 grados. Este concepto, conocido como la propiedad de la suma de ángulos internos de un triángulo, es fundamental para resolver cualquier problema relacionado con los ángulos de esta figura geométrica.
Paso 1.1: Triángulo equilátero
Para un triángulo equilátero, donde todos los lados tienen la misma longitud, cada ángulo interior será de 60 grados. Dado que la suma de los tres ángulos es 180 grados, cada ángulo en un triángulo equilátero será de 60 grados.
Paso 1.2: Triángulo escaleno
En un triángulo escaleno, donde todos los lados tienen longitudes diferentes, el cálculo de los ángulos puede ser más complejo. Se puede utilizar la ley de los cosenos para determinar cada uno de los ángulos internos.
Paso 2: Utilizar la ley de los cosenos
La ley de los cosenos es una herramienta matemática poderosa que nos permite calcular los ángulos de un triángulo cuando conocemos las longitudes de sus lados. Esta ley establece una relación entre los lados y ángulos de un triángulo y se expresa de la siguiente manera:
[ c^2 = a^2 + b^2 – 2ab cdot cos(C) ]
Donde ( a ), ( b ) y ( c ) representan las longitudes de los lados del triángulo, y ( C ) es el ángulo opuesto al lado de longitud ( c ).
Paso 3: Ejemplo práctico
Supongamos que tenemos un triángulo con lados de longitudes ( a = 5 ), ( b = 7 ) y ( c = 8 ). Para encontrar el ángulo opuesto al lado de longitud 8, que llamaremos ( C ), podemos aplicar la ley de los cosenos de la siguiente manera:
[ 8^2 = 5^2 + 7^2 – 2 cdot 5 cdot 7 cdot cos(C) ]
[ 64 = 25 + 49 – 70 cdot cos(C) ]
[ 64 = 74 – 70 cdot cos(C) ]
[ cos(C) = frac{74 – 64}{70} ]
[ cos(C) = frac{10}{70} ]
[ cos(C) = frac{1}{7} ]
Por lo tanto, el ángulo ( C ) es igual al arcocoseno de ( frac{1}{7} ).
¿Se pueden utilizar otras fórmulas para encontrar los ángulos de un triángulo?
Sí, además de la ley de los cosenos, existen otras fórmulas y propiedades geométricas que pueden ayudarte a calcular los ángulos de un triángulo. Algunas de las más comunes incluyen la ley de los senos, el teorema del seno y el teorema del coseno.
¿Es importante conocer los ángulos de un triángulo en la vida cotidiana?
Aunque puede parecer un concepto matemático abstracto, comprender los ángulos de un triángulo puede tener aplicaciones prácticas en diversas situaciones, como la construcción, la navegación y la resolución de problemas de ubicación. ¡Nunca subestimes el poder de la geometría en la vida diaria!