La pendiente de una recta es un concepto fundamental en la geometría analítica y el álgebra, que nos permite comprender la inclinación de una recta en un plano cartesiano. En esta guía completa, exploraremos de forma sencilla cómo se representa y calcula la pendiente de una recta, paso a paso, para que puedas dominar este concepto de manera clara y concisa.
Concepto de pendiente y su importancia
Antes de sumergirnos en los detalles de cómo calcular la pendiente de una recta, es crucial comprender qué representa este valor y por qué es tan relevante en matemáticas. La pendiente de una recta indica la inclinación de la misma, es decir, cuánto se eleva o desciende en función del desplazamiento horizontal. Es un factor determinante en la relación entre dos puntos de una recta y nos brinda información sobre la dirección y la intensidad del crecimiento de la función lineal representada por dicha recta.
Cálculo de la pendiente a partir de dos puntos
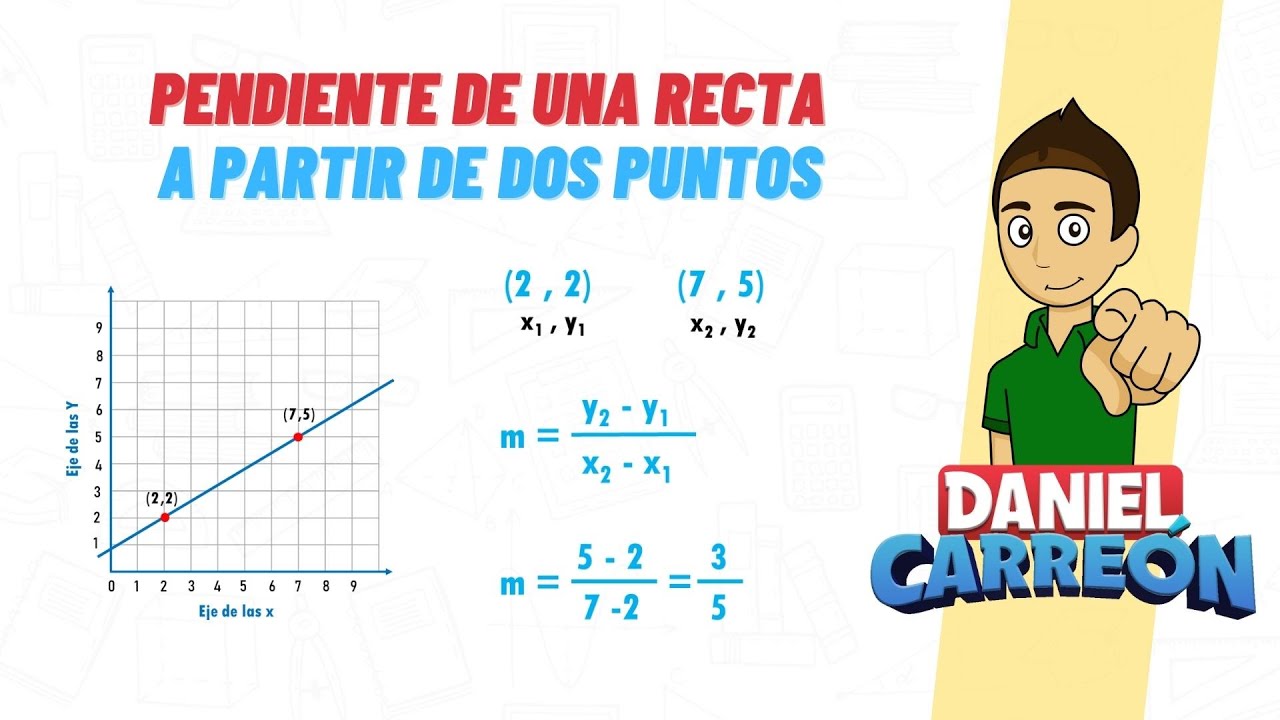
Una de las formas más comunes de determinar la pendiente de una recta es utilizando la fórmula que involucra dos puntos específicos en el plano cartesiano. Para ello, necesitamos identificar las coordenadas de estos dos puntos, que representaremos como (x1, y1) y (x2, y2). La fórmula general para calcular la pendiente m se expresa como:
[ m = frac{y_{2} – y_{1}}{x_{2} – x_{1}} ]
Donde la diferencia en las coordenadas y dividida por la diferencia en las coordenadas x nos da el valor de la pendiente. Este método es útil y eficaz para determinar la inclinación de una recta cuando se conocen dos puntos específicos en su trayectoria.
Otras formas de calcular la pendiente
Además del método de los dos puntos, existen otras formas de calcular la pendiente de una recta en situaciones específicas. Por ejemplo, cuando se tiene la ecuación de la recta en su forma general y = mx + b, el valor de m representa la pendiente de la recta. En este caso, la pendiente es el coeficiente que acompaña a la variable x en la ecuación de la recta. De esta manera, podemos obtener la pendiente directamente a partir de la ecuación de la recta, sin necesidad de recurrir a puntos concretos.
Inclinación positiva y negativa
Es importante destacar que la pendiente de una recta puede ser tanto positiva como negativa, lo que indica la dirección en la que la recta se inclina en el plano cartesiano. Cuando la pendiente es positiva, la recta se eleva de izquierda a derecha, mientras que una pendiente negativa señala un descenso en esa misma dirección. Estas diferencias en la pendiente son fundamentales para interpretar el comportamiento de una recta y su relación con las variables que representa.
Interpretación geométrica de la pendiente
Desde un punto de vista geométrico, la pendiente de una recta se relaciona directamente con el ángulo de inclinación que esta forma con el eje horizontal. Cuanto mayor sea el valor absoluto de la pendiente, más pronunciada será la inclinación de la recta en el plano. Esta interpretación geométrica nos permite visualizar de manera intuitiva cómo se comporta una recta en función de su pendiente, facilitando la comprensión del concepto desde una perspectiva espacial.
Aplicaciones prácticas de la pendiente
La pendiente de una recta no solo se limita al ámbito matemático, sino que tiene numerosas aplicaciones prácticas en diversos campos, como la física, la ingeniería, la economía y la geografía. Por ejemplo, en física, la pendiente puede representar la velocidad de un objeto en movimiento, en tanto que en economía, puede indicar la tasa de crecimiento de un mercado. Comprender cómo calcular y interpretar la pendiente de una recta es fundamental para abordar problemas reales y tomar decisiones informadas en diferentes contextos.
¿Qué significa una pendiente nula en una recta?
Cuando la pendiente de una recta es igual a cero, significa que la recta es horizontal y no presenta ninguna inclinación vertical. En este caso, la ecuación de la recta será de la forma y = b, donde b es el valor de la ordenada al origen.
¿Cómo puedo visualizar la pendiente de una recta en un gráfico?
Para visualizar la pendiente de una recta en un gráfico, basta con trazar la recta y observar la inclinación que presenta con respecto al eje horizontal. Cuanto más inclinada esté la recta, mayor será su pendiente.
¿Por qué es importante calcular la pendiente de una recta en el ámbito empresarial?
Calcular la pendiente de una recta en el ámbito empresarial puede ofrecer información crucial sobre el rendimiento de un negocio, la evolución de sus ingresos o la eficiencia de sus operaciones. Esta medida puede ayudar a identificar tendencias, proyectar crecimientos futuros y optimizar estrategias empresariales.
En conclusión, la pendiente de una recta es un concepto matemático fundamental con aplicaciones extendidas en diversos campos. Dominar el cálculo y la interpretación de la pendiente nos permite comprender mejor la relación entre variables, predecir comportamientos y tomar decisiones fundamentadas. ¿Listo para explorar el fascinante mundo de las rectas y sus pendientes? ¡Adelante y sigue descubriendo nuevas formas de representar la realidad a través de las matemáticas!